Title: Predict the output of the function program based on the input parameters

Abstract:

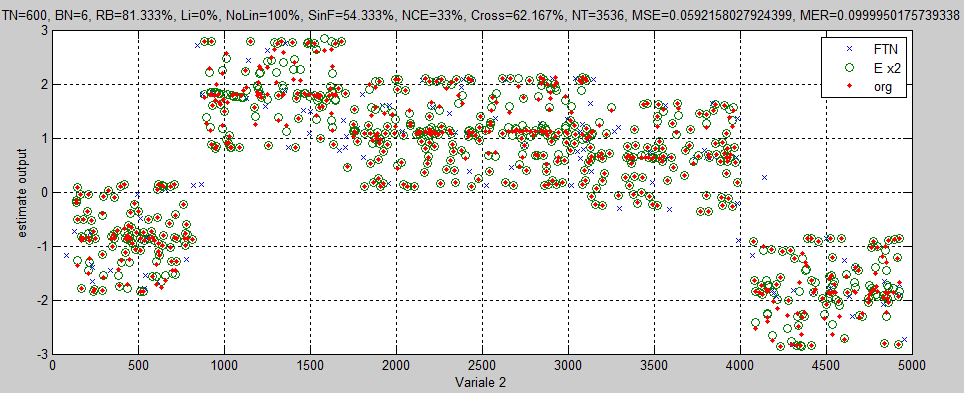
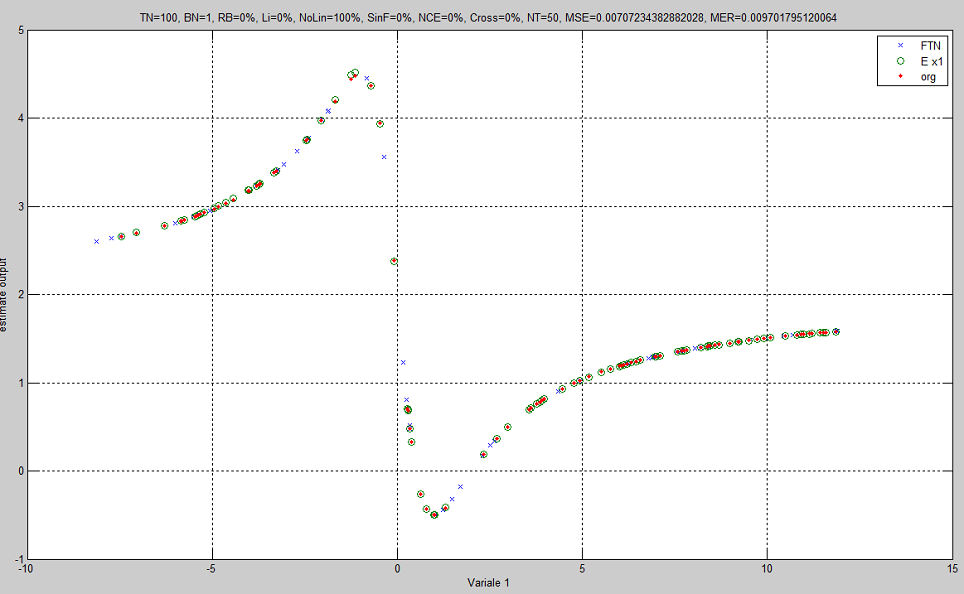
This paper aims to approximate the numerical result of executing a program/function with some input parameters and a single output value with a small number of training points. Curve fitting methods are preferred to non-deterministic methods such as neural network and fuzzing system methods because they can provide relatively more accurate results with the less amount of members in the training dataset. However, curve fitting methods themselves are most often function-specific and do not provide a general solution to the problem. These methods are most often targeted at fitting specific functions to their training dataset. To provide a general curve fitting method, in this paper, the use of a combination of Lagrange, Spline, and trigonometric interpolation methods is suggested. The Lagrange method fits polynomial functions of degree N to its training values. To improve the resultant fitted polynomial, our combinatorial method combines Lagrange with the polynomial resulted from the Spline method. If the absolute error of the actual value and the predicted value of a function, is not desired, the trigonometric interpolation methods that fit trigonometric functions can be applied. Our experiments with several benchmark examples demonstrate the relatively high accuracy of our combinational fitting method.

Keyword:

Output approximation, Curve fitting, Linear state approximation, Nonlinear state approximation.